Natural numbers (N) : 1, 2, 3 … 자연수
Whole number (W) : 0, 1, 2, 3 … 정수
Integers (Z) : -2, -1, 0, 1, 2 …
Rational numbers (Q) … 유리수
Irrational numbers … 무리수
Real numbers (R) … 실수
Complex numbers (C) … 허수
fraction 분수
numerator 분자
denominator 분모
reciprocal
y is 5 over 3 : y=5/3. 삼분의 오
y is 2 over 5 : y=2/5. 오분의 이
y is 1 over x : y=1/x. y는 x분의 일
Commutative Property of Addition: a+b = b+a 덧셈에 대한 교환법칙
Commutative Property of Multiplication: a*b = b*a 곱셉에 대한 교환법칙
Associative Property of Addition: (a+b)+c = a+(b+c) 덧셈에 대한 결합법칙
Associative Property of Multiplication: (a*b)*c = a*(b*c) 곱셈에 대한 결합법칙
Distributive Property: a*(b+c) = a*b + a*c 곱셈에 대한 분배법칙
Linear Equation (Simple Equation) 1차 방정식
intercept 절편
slope 기울기
axis 축
parallel line 평행선
perpendicular line 수직선
slop-intercept Form y=mx+b
point-slope from y-y0=m(x-x0)
quotient 몫
perimeter 둘레
parabola 포물선
domain 정의역
range 치역
x-coordinate x좌표
y-coordinate y좌표
costant 상수
quadratic functions 2차함수, 이차함수
cubic functions 3차함수, 삼차함수
rational functions 유리함수
- 정의역(domain): x≠0, (-∞, 0) ∪ (0, ∞), x는 0이 아닌 모든 실수(Real numbers)
- 치역(range): y≠0
- x-intercept and y-intercept = ≠ n/a
irrational functions 무리함수 (x>0)
absolute value functions 절대값함수
- Domain = R
- Range = [0, ∞)
- x-intercept and y-intercept = (0,0)
exponential functions 지수함수
- base 'a': a>1, increasing / 0<a<1, decreasing
- D = R
- R = y>0 (0, ∞)
- y-intercepts: (0,1)
- x-intercepts: y=0
- 'one-to one' function
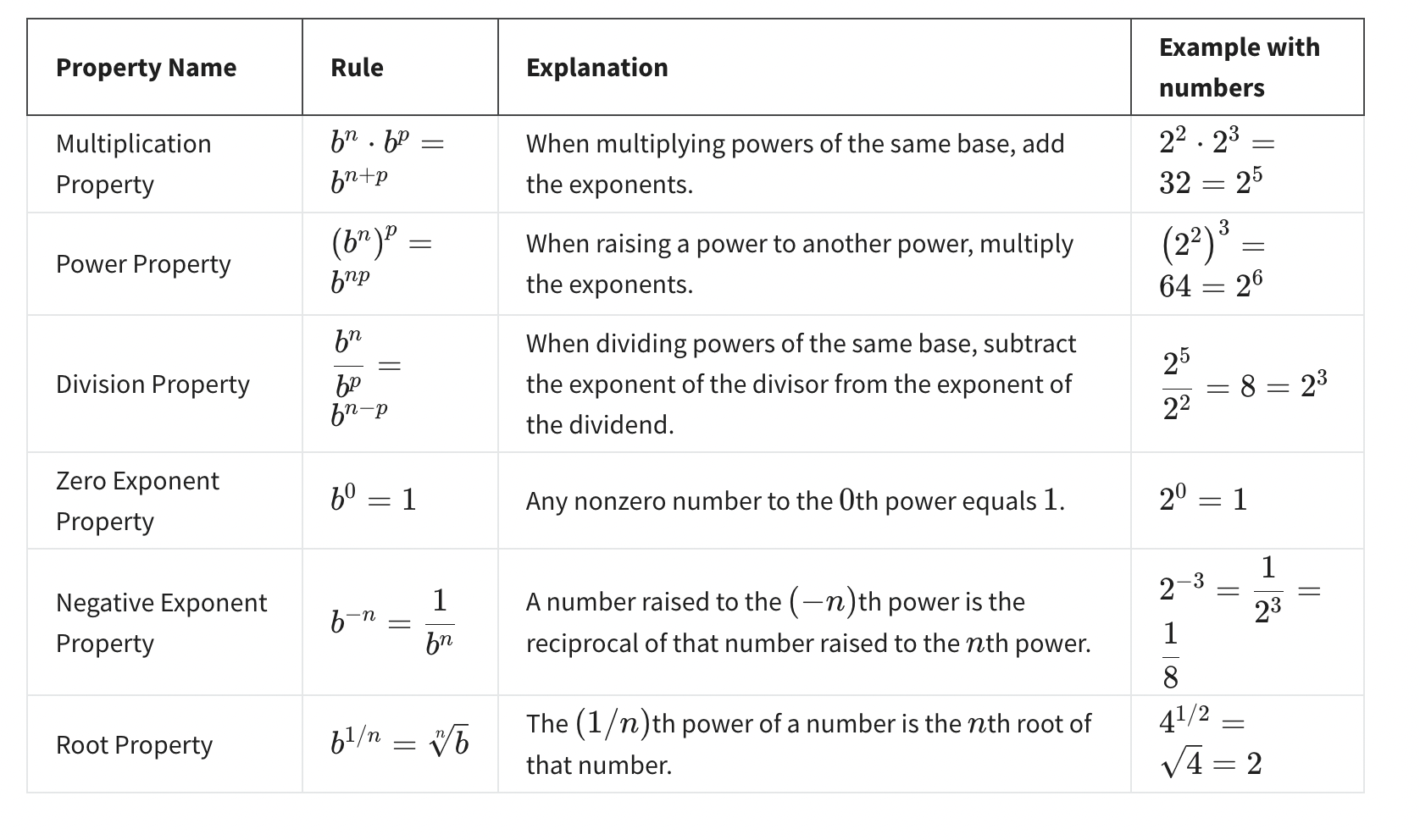
& logarithms functions 지수함수와 로그함수
greatest integer functions (floor functions) 가우스함수, 최대정수함수, always round down.
- Domain = Real numbers
- Range = Z(integers)
piecewise functions 개별식함수, 분할함수
- D = R
- Range = R
trigonometrical functions 삼각함수
- sin x, cos x, tan x
- D = R
- R = [-1, 1]
the unit circle 원의 방정식
- x2+y2 = r2
function composition 합성함수
- f˚g = (f˚g)(x) = f(g(x)) : 뒤에것부터 먼저.
- f˚g˚h = f(g(h(x)))
- f˚g ≠ g˚f



one-to-one 일대일함수
- a function is 'one-to-one' if no two different inputs correspond to the same output.
compound interest 복리 (exponential function)
polynomial 다항식의
coefficient 계수
right triangle 직각삼각형
e ≒ 2.718...
- irrational real numbers
Simple Interest 단리
- It is typically used for short-term loans, such as auto loans.
- Let P be the principal amount and let r% be the simple interest rate. Then if interest is added t times, the total amount of interest added is given by the formula.
- simple interest = P*r/100*t = P(0.01r)t
- and the total amount is P(1+rt/100) = P(1+0.01rt)
Compound Interest 복리
댓글